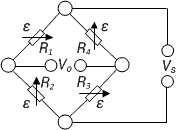
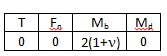
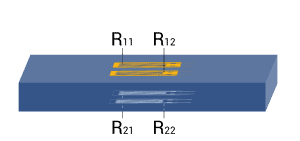
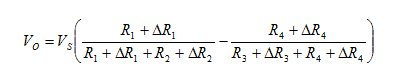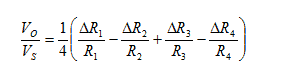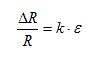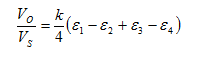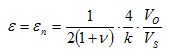arrow_back_ios
Main Menu
arrow_back_ios
Main Menu
- Mechanical & structural DAQ systems
- Sound & Vibration DAQ systems
- Industrial electronics
- Simulator Systems
- Electric power analyzers
- S&V Handheld devices
- Wireless DAQ Systems
- DAQ
- Drivers API
- nCode - Durability and Fatigue Analysis
- ReliaSoft - Reliability Analysis and Management
- Test Data Management
- Utility
- Vibration Control
- Inertial Sensor Software
- Test Data Management
- Asset Monitoring
- Sensor Finder
- Acoustic
- Current / voltage
- Displacement
- Exciters
- Force
- Inertial Sensors
- Load cells
- Multi Component
- Pressure
- Smart Sensors with IO-Link interface
- Strain
- Fiber Optic Temperature Sensors
- Fiber Optic Tilt Sensors
- Torque
- Vibration
- OEM Custom Sensors
- Calibration Services for Transducers
- Calibration Services for Handheld Instruments
- Calibration Services for Instruments & DAQ
- On-Site Calibration
- Resources
- Articles
- Case Studies
- Recorded Webinars
- Primers and Handbooks
- Videos
- Whitepapers
- Search all resources
- Acoustics
- Data Acquisition & Analysis
- Durability & Fatigue
- Electric Power Testing
- Industrial Process Automation
- Machine automation control and navigation
- NVH
- Reliability
- Smart Sensors
- Structural Health Monitoring
- Vibration
- Virtual Testing
- Weighing
- Road Load Data Acquisition
arrow_back_ios
Main Menu
- QuantumX
- SomatXR
- MGCplus
- Optical Interrogators
- CANHEAD
- eDAQ
- Strain Gauge precision instrument
- Bridge calibration units
- GenHS
- LAN-XI
- Fusion-LN
- CCLD (IEPE) signal conditioner
- Charge signal conditioner
- Microphone signal conditioner
- NEXUS
- Microphone calibration system
- Vibration transducer calibration system
- Sound level meter calibration system
- Accessories for signal conditioner
- Accessories for calibration systems
- Multi channel amplifier
- Single channel amplifier and amplifier with display
- Weighing indicators
- Weighing electronics
- Accessories for industrial electronics
- eDrive power analyzer
- eDrive Package - Remote Probe based
- eGrid power analyzer
- GenHS
- Accessories for power analyzer and GenHS
- BK Connect / PULSE
- Tescia
- Catman data acquisition software
- Thousands of Channels at a Glance
- Perception – High speed data acquisition software
- Drivers for compatibility with third party software
- ReliaSoft BlockSim
- ReliaSoft Cloud
- ReliaSoft Lambda Predict
- ReliaSoft MPC
- ReliaSoft Product Suites
- ReliaSoft RCM++
- ReliaSoft XFMEA
- ReliaSoft XFRACAS
- ReliaSoft Weibull++
- Classical Shock
- Random
- Random-On-Random
- Shock Response Spectrum Synthesis
- Sine-On-Random
- Time Waveform Replication
- Vibration Control Software
- Microphone sets
- Cartridges
- Reference microphones
- Special microphones
- Acoustic material testing kits
- Acoustic calibrators
- Hydrophones
- Microphone Pre-amplifiers
- Sound Sources
- Accessories for acoustic transducers
- Fiber Optic Technology
- Inductive technology
- Strain gauge technology
- Accessories for displacement sensors
- Inertial Measurement Units (IMU)
- Vertical Reference Units (VRU)
- Attitude and Heading Reference Systems (AHRS)
- Inertial Navigation Systems (INS)
- Inertial Sensor Accessories
- Bending / beam
- Canister
- Compression
- Single Point
- Tension
- Weighing modules
- Digital load cells
- Accessories for load cells
- Strain gauges for experimental testing
- Fiber optical strain gauges
- Strain gauges for transducer manufacturing (OEM)
- Strain sensors
- Accessories for strain gauges
- Accelerometers
- Force transducers
- Impulse hammers / impedance heads
- Tachometer probes
- Vibration calibrators
- Cables
- Accessories
- Force - OEM custom sensors
- Torque - OEM custom sensors
- Load - OEM custom sensors
- Multi-Axis - OEM custom Sensors
- Pressure - OEM custom sensors
- HATS (Head and torso simulator)
- Artificial Ear
- Electroacoustic hardware
- Bone conduction
- Electroacoustic software
- Pinnae
- Accessories for electroacoustic application
- Accessories
- Actuators
- Combustion Engines
- Durability
- eDrive
- Mobile Systems
- Production Testing Sensors
- Transmission Gearboxes
- Turbo Charger
- Force Calibration
- Torque Calibration
- Microphones & Preamplifiers Calibration
- Accelerometers Calibration
- Pressure Calibration
- Displacement Sensor Calibration
- Sound Level Meter Calibration
- Sound Calibrator & Pistonphone Calibration
- Vibration Meter Calibration
- Vibration Calibrator Calibration
- Noise Dosimeter Calibration
- QuantumX Calibration
- Genesis HighSpeed Calibration
- Somat Calibration
- Industrial Electronics Calibration
- LAN-XI Calibration
- Guidelines on Calibration Intervals
- Certificate Samples
- Interactive Calibration Certificate
- Download of Calibration Certificates
- Acoustics and Vibration
- Asset & Process Monitoring
- Data Acquisiton
- Electric Power Testing
- Fatigue and Durability Analysis
- Mechanical Test
- Reliability
- Weighing
- Electroacoustics
- Noise Source Identification
- Handheld S&V measurements
- Sound Power and Sound Pressure
- Noise Certification
- Acoustic Material Testing
- Structural Durability and Fatigue Testing
- Durability Simulation & Analysis
- Material Fatigue Characterisation
- Electrical Devices Testing
- Electrical Systems Testing
- Grid Testing
- High-Voltage Testing
- End of Line Durability Testing
- Vibration Testing with Electrodynamic Shakers
- Structural Dynamics
- Machine Analysis and Diagnostics
- Troubleshooting Analyser
- Naval Certification and Sea-Trials
- Process Weighing
- Sorting and Batching Solutions
- Scale Manufacturing Solutions
- Vehicle Scale Solutions
- Filling, Dosing and Checkweighing Control
arrow_back_ios
Main Menu
- Housing
- Communication processor
- Amplifier modules
- Connection boards
- Special function modules
- Accessories for MGCplus
- Binaural Audio
- Outdoor microphones
- Probe Microphones
- Sound intensity probes
- Surface microphone
- Array microphones
- Other special microphones
- Microphones for production line test
- Probe microphones
- Microphone Cables
- Tripods
- Microphone booms
- Microphone adapters
- Electrostatic actuators
- Microphone windscreen
- Nose cones
- Microphone holders
- Other accessories for acoustic transducers
- Microphones outdoor protection
- Rod end bearings
- Tensile load introductions
- Thrust pieces and load buttons
- Cables and connectors
- Screw sets
- Load bases / Tensile compressive adapters
- Measurement cables
- Ground cables
- Thrust pieces
- Bearings
- Load feet
- Base plates
- Knuckle eyes
- Adapters
- Mounting aids and others
- Adhesives
- Protective coatings
- Cleaning material
- SG Kits
- Solder terminals
- Other strain gauge accessories
- Cables
- ZeroPoint Balancing
- TCS Balancing
- TC0 Balancing
- Magnets
- Mounting clips/bases
- Studs, screws and washers
- Adhesives/Tools
- Adapters
- Mechanical filters
- Other accessories
- High-Force LDS Shakers
- Medium-Force LDS Shakers
- Low-Force LDS Shakers
- Permanent Magnet Shakers
- Shaker Equipment / Slip Tables
- Testing Of Hands-Free Devices
- Smart Speaker Testing
- Speaker Testing
- Hearing Aid Testing
- Headphone Testing
- Soundbar Testing
- Telephone Headset And Handset Testing
- Acoustic Holography
- Acoustic Signature Management
- Underwater Acoustic Ranging
- Wind Tunnel Acoustic Testing – Aerospace
- Wind Tunnel Testing For Cars
- Beamforming
- Flyover Noise Source Identification
- Real-Time Noise Source Identification With Acoustic Camera
- Sound Intensity Mapping
- Spherical Beamforming
- Product Noise
- HighVoltage HighPower Switchgear Tests
- Transformer Testing
- Current Zero Testing
- Circuit Breaker Testing
- Messung der Unrundheit von Eisenbahnrädern
- On-Board Measurement
- Pantograph and Overhead Lines Monitoring
- Wayside Train Monitoring & Measurement
- Shock and Drop Testing
- Environmental Stress Screening - ESS
- Package Testing
- Buzz, Squeak and Rattle (BSR)
- Mechanical Satellite Qualification - Shaker Testing